At JW Player our analytics pipeline currently receives 4M pings per minute at peak times, providing the basis for insights to the publishers on our dashboards. Recently we have moved some of our offline classification processes to the beginning of our real-time and batch pipelines, which required us to optimize our string matching implementations. We employed finite state automata, rolling hash functions, and bloom filters to achieve 6x and 3x speedup in NSFW classification and ad classification respectively. In this article, we will discuss these classification problems, then the algorithms, implementations, as well as evaluation of our solutions.
Our player is freely available, and we strive to provide the best analytics experience to all the publishers who use our player.
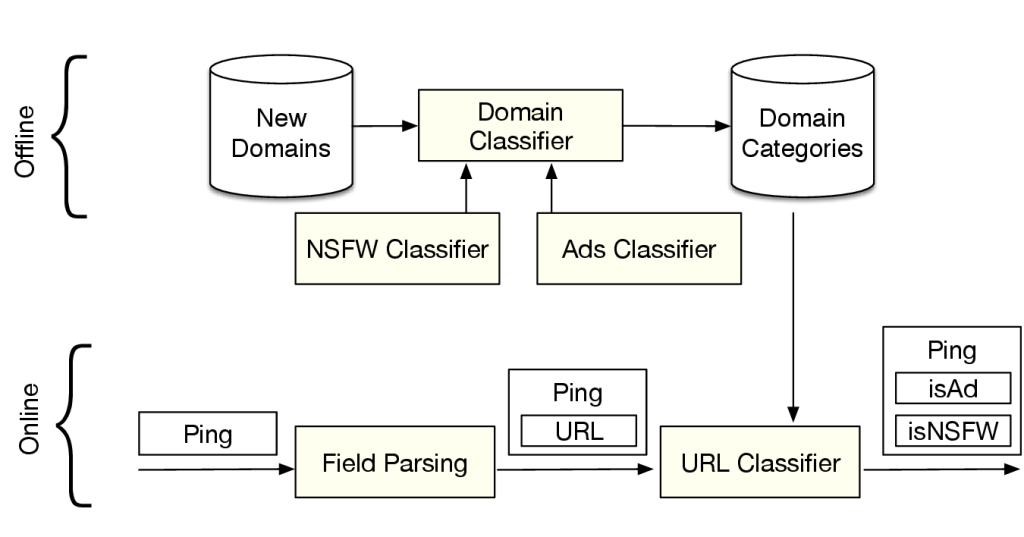
One of the questions that we ask about these pings is the category of the publisher’s content. The first thing we check is whether a publisher has been serving ads instead of video content using our player, or whether the publisher is serving NSFW content. We are looking to make this distinction in order to have a better understanding of the content spectrum in our network, and to better guide our efforts to plan and improve our existing services.
Performance Needs
JW Analytics Pipeline in Morrigan’s blog post explains the various steps in which we progressively process the incoming pings. The Ping Parser is the first step we perform on the pings before doing any further processing. For batch processing, the periodic batch pipelines have to keep up with 4 Billion ping requests per day, and the real-time pipeline has to keep up with 4 Million requests per minute. Roughly this translates to a minimum throughput requirement of 1M pings/86.4sec for daily batch processing, and 1M pings /15sec for real-time processing. We exploit parallelism in our architectures to address such demands. We also employ lazy evaluation for the types of processing which have heavy computational requirements, i.e. we delay the processing of some fields till an aggregate of the data is available, or limit the processing on a particular slice of the data.
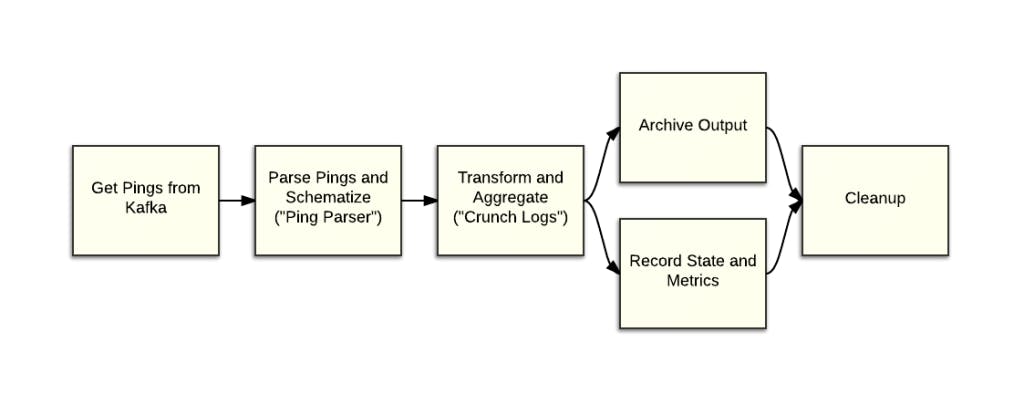
Figure 1: Periodic Batch Pipeline
The specs for the compute nodes that we use differ, depending on whether they are used in real-time or batch, as well as their roles in the respective topologies, however more memory and more processing power means more compute cost. Generally speaking, we are not only looking to add more insight to the data as early as possible, but also looking to keep the cost of such processing at a minimum, so a desirable solution needs to operate with as little memory as possible. Adding resource intensive implementations of classification to the early stages of our pipelines would have required prohibitive amount of scaling horizontally or vertically to make up for the additional resource needs, which made us explore efficient algorithms and optimized implementations. Profiling and benchmarking tools provided us the necessary comparison guidance in this exploration. We discuss these tools in the Benchmarks section.
Domain matching
When a new domain is seen for the first time, we set out a process in the daily batch pipeline to assign a category to the domain. Along with publicly available data about domains, this offline process yields a large list of domains and their category labels. We then use these domain categories to assign a field in the ping schema as NSFW.
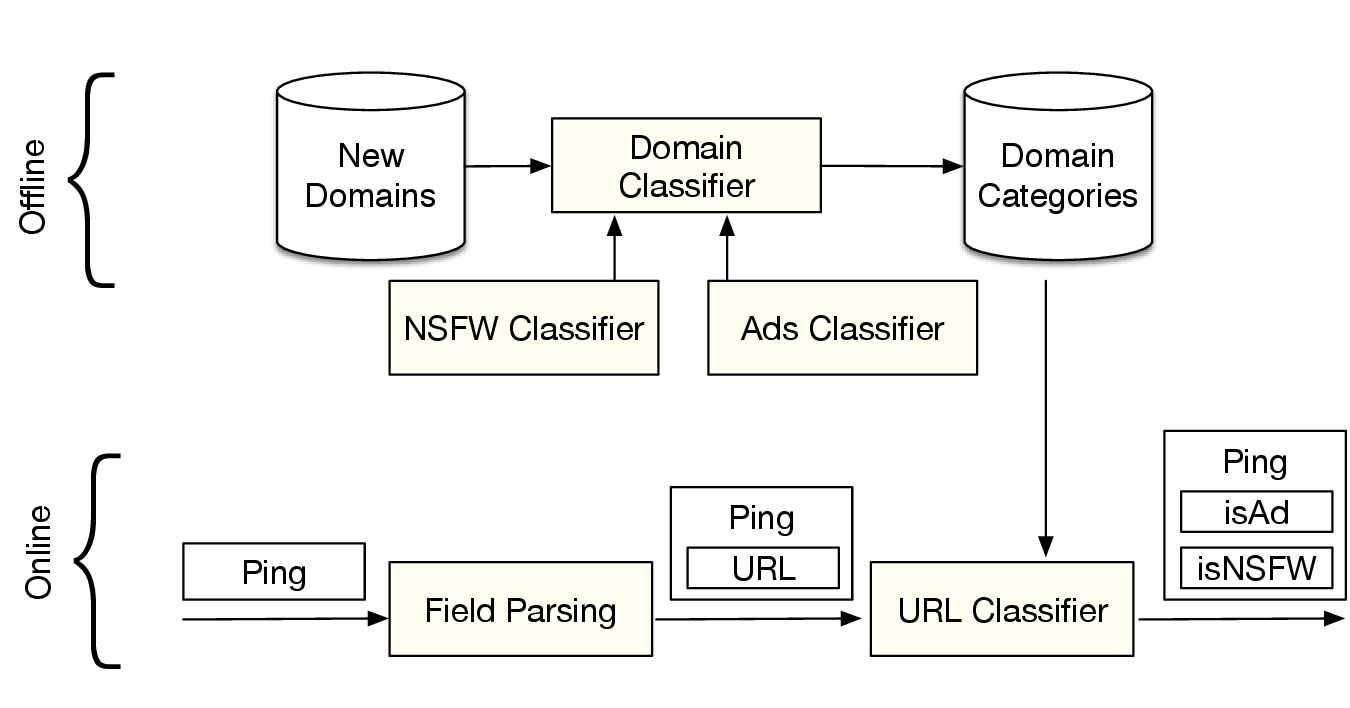
Figure 2: Domain List update and query
Domain matching is a very common string matching problem that we solve regularly, however the scale of the problem in our case requires special attention. The list of known domains and their categories can grow arbitrarily large to millions of domains, which puts stress on the available memory.
The commonly used approach is to use a HashSet (or similar hash structure) to store the list of domains in an easy to look up manner. This approach has two shortcomings that make it less attractive for our use: i) even though a hash is very effective for smaller lists, storing millions of domain strings in memory quickly becomes a bottleneck, ii) more critically, hash lookups require an exact match, which means we need to extract all the domain names that could possibly be an exact match from the URL string before being able to query the blacklist.
The problem with exact matching is that, some blacklist entries may refer to top-level private domain names, whereas others refer to subdomains, or to public suffixes which may also be private domains. The Guava documentation provides a nice review of the internet domain names and public suffixes. In short, the list of public suffixes is not limited to a handful of country-specific exceptions, and is as extensive as the number of services that allow their users to own a subdomain under their domain name. In the example of Figure 3, amazonaws.com, s3.amazonaws.com, and jwplayer.s3.amazonaws.com could potentially have labels and have to be checked seperately. When we use hash tables, not only do we need to parse these different level domain names from the hostname string, we also need to query the hash table multiple times to see if any of these domain names are included in the table. And, if we are not careful about public suffixes, we might never match some values.
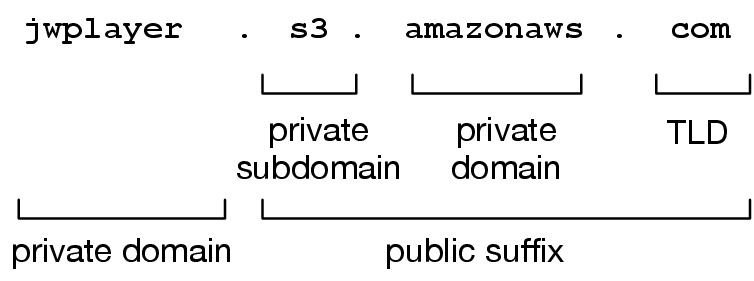
Figure 3: Public suffixes, top-level domains, and top-level private domains
Have the cake and eat it too: Domain Name Automaton
Fortunately, we can match all the different levels of domain naming conventions at once, and do it fast, and also use even less memory.
We first observe that the domain names are hierarchical when the domain names are read from right to left. And when the hostname strings are processed in a right-to-left walk on its characters, the matches at the public domain suffix, toplevel domain name, or the subdomain name all occur at the domain name boundary marked with a . character or at the end of hostname string. Unfortunately this is not sufficient to solve our problem, because we still need to be able to match a prefix of the reverse string to the list of domains in our table instead of an exact match.

Figure 4: Right-to-Left traversal of hostname
The perfect tool in our arsenal for the prefix matching is the simple yet powerful finite state automaton. We will not go into technical details of finite state automaton, but we need to know a few concepts to understand how this matching method works. Generally speaking, a finite state automaton is defined on a finite alphabet A, and a finite set of states Q, one of which is a start state, and a subset of which are accept states. Arcs or transitions are triplets from the set QxAxQ, and provide the instructions for the automaton to change its current state to another state upon seeing an input character in the alphabet.
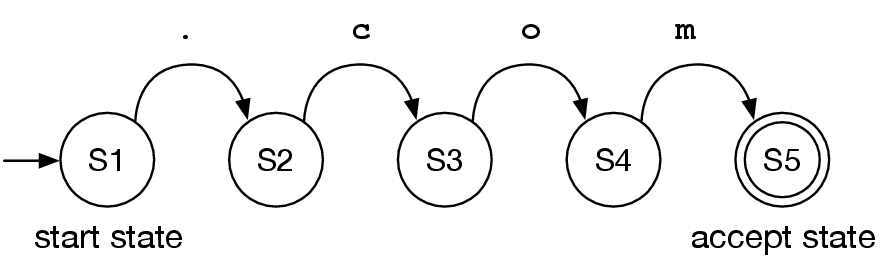
Figure 5: Finite state automaton that accepts string “.com”
We will demonstrate the use of automata with OpenFST on a set of domains. The OpenFST library is available for download from http://www.openfst.org and is released under the Apache license.
We create an OpenFST acceptor automaton by adding all the domains.

Figure 6: Non-deterministic domain automaton
Our acceptor automaton is very inefficient at this point, since it is simply a non-deterministic automaton which immediately branches out to n disjoint paths with an epsilon-transition at the start state. OpenFST has tools to remove the epsilon-transitions and to determinize our automaton.
Figure 7: Determinized automaton
At this stage, the prefixes of the strings are compressed, similar to a trie. However, suffixes are still not compressed. OpenFST’s minimization uses Dominique Revuz’s Minimization of Acyclic Deterministic Automata in Linear Time to minimize the automata in linear time. The resulting automaton is a very compact representation of the input strings.

Figure 8: Minimized automaton
As a last step of this demonstration, we reverse the automaton to show how we keep our automata for right-to-left domain matching. After this step, we convert the optimized automaton into a format, which can then be easily read for further use in our processing pipelines.

Figure 9: Reversed Minimized automaton.
Going back to our initial objective of matching domains, notice how easy it is to take any hostname string and traverse the automaton right to left. Whenever the automaton does not have a transition to match our input, we will immediately know that the hostname we are considering is not in the list of domains we are matching, even without going through the complete hostname string once. This property is particularly useful in languages like Java, where substring operations are costly, yet character-by-character traversals are relatively cheap. Finally if our traversal reaches a final state, we need to check whether the hostname string is consumed completely or we have reached a domain name boundary, the . character.
We will discuss the performance of the implementation in the Benchmarks section.
Ad Detection
Our video player is sometimes used to embed ad content into pages. As these ads could potentially reach high volumes in a way that could consume our computing resources, we look to detect pings from such players as early as possible. Unfortunately, the domain matching has only limited success in finding these players, so we turn to effective ad detection methods that are used by browser ad blockers, such as Easylist.
Easylist consists of a set of rules, some of which are written in a custom regular expression format as described in this AdBlockPlus blog post. Several AdBlock blog posts evaluate different matching algorithms suitable for Easylist, and report improvements.
The method that we use is based on matching substrings of the regular expression rules to a given URL. This allows us to decide whether it is plausible that a given URL would match one of the Easylist rules. If we find a substring match, we then proceed to the more expensive step of verifying the match by applying the regular expression rules that share the matched substring.
Our strategy for performance improvement is to make the decision about whether a given ping is a plausible Easylist match as fast as possible, as this step will be performed on all pings. If only a small set of pings are coming from URLs that match Easylist rules, then we should see a jump in the performance of a naive implementation that doesn’t optimize the plausible matching step.
The substrings that we consider have a constant length. We prefer this length to be large, because larger strings have a smaller probability of matching by chance, and we prefer to avoid consulting the expensive regular expression matching as much as possible.
The general method of substring matching involves inspecting a sliding window over the characters of the string we are looking to match. The window at position j of the string s, checks whether the substring s[j, j+l-1] is in our pattern table.
Myriad Virtues of Automata: Substring Matching
A simple implementation of the sliding window matching with hash tables would require us to create new String objects from every sliding window, and query each of them with the hash table. The automaton that we discussed in the Domain Matching section had the ability to check for matches character by character. However, in that case we were only growing the string from one side, and in a sliding window, we should also forget characters that have slid outside of the window. Everytime we cannot match a character in a window, we slide the window by one, reset our input position to the beginning of the window, and restart traversing the automaton back from the start state. This feels like Sisyphus trying to carry the boulder up a hill, only to see it roll back again.
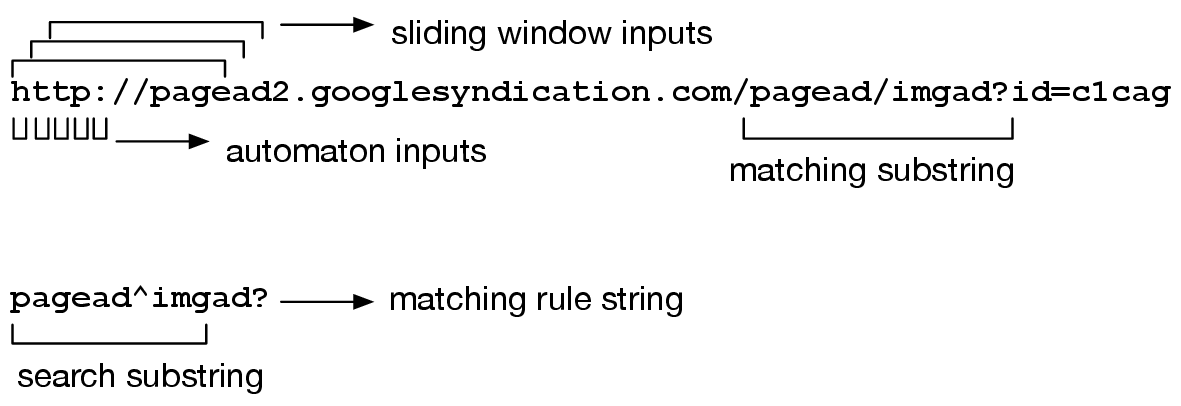
Figure 10: Sliding window search for plausible rule matches
A little bit of automata theory will break the curse of Sisyphus on our substring automaton. We are going to build an automaton for which, there will be transitions for every input character in all states. This will make sure that whenever we see an input character, we will always have a state to go to, without having to scroll back our input to the beginning of the sliding window.
Assume that we have two words in our table: sell and else. In the desired automaton, if we have seen the character sequence sel, that is not followed by l, but an s and e, the automaton will take the transition to a state that accepts the word else instead, remembering the fact that characters e and l were just consumed. Instead of the Aho-Korasick algorithm which constructs such automata, we use OpenFST which we used for compiling the domain automaton in the previous section.
The construction of the substring match automaton uses an interesting automaton operation. We first build a word automaton for the patterns that we are looking to match, the same way we built the domain automaton, skipping the reversal of the automaton in the final step, as we will be scanning strings left-to-right. Then we define another automaton that accepts all strings in the alphabet A, usually called an A* automaton. When we concatenate the word automaton to the A* automaton, we have a non-deterministic automaton that will not need to scroll back, as there will always be a transition to take for any input character (see Figure 11). Finally, determinization and minimization of the resulting automaton will give us an efficient automaton that we can just keep traversing with the input string, as in Figure 12. When the traversal hits an accept state we can be sure that the string includes a match in our table. In the example with words sell and else, our alphabet consists of only three letters, A={e,l,s}.
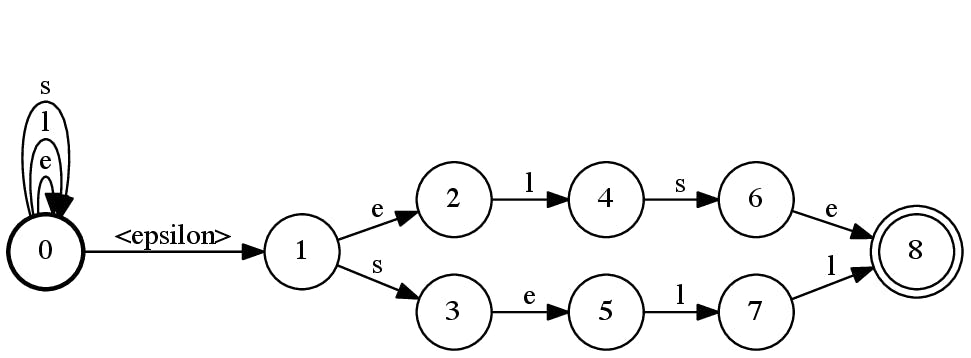
Figure 11: Concatenation of A* and the word automata for {else, sell}
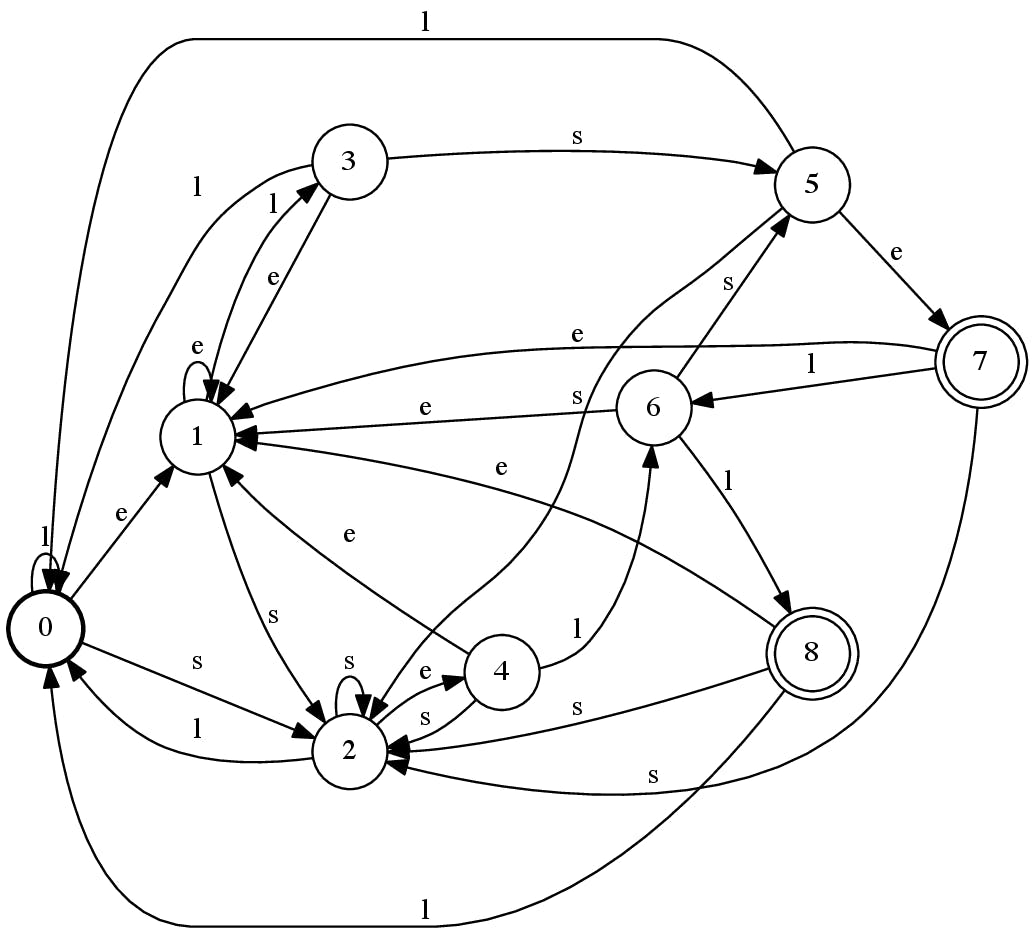
Figure 12: Substring search automaton for “sell” and “else”
The use of an automaton for matching has another added benefit in this case. Remember, when the automaton matches a rule substring, we still cannot say whether the string would match the associated Easylist rule(s). This means, we still need to fetch the set of rules from memory after finding the matching substring, usually implemented using, you guessed it, a hash table. A neat optimization here is to assign state id values in the automaton, such that all the k accept states have consecutive numbers in [1,k]. This way, each substring match will have a unique accept state id, which we can use to store the set of rules associated with the substring match. The method is similar to Minimal Perfect Hashing as described in Lucchesi et. al..
Another, perhaps more important, optimization is regarding the number of transitions in the A*B automaton; this automaton has transitions for all valid input characters, and a significant portion of these transitions go back to the start state. Even in the artificially small and compact example of Figure 12, states 0,2,3,5,8 all have a transition back to start state for input l. We can omit these transitions to reduce the memory requirements of this automaton without impacting the running time of the algorithm.
Substring Matching with Hashes
Rabin-Karp algorithm presents an elegant solution to parallel matching of strings through the use of fingerprints. Instead of comparing strings x and y, we compare hash(x) and hash(y), where i) hash() computation is efficient, and ii) if hash(x) = hash(y) then x=y with high probability. The hash function used in Rabin-Karp algorithm can efficiently compute the next hash value of the sliding window from the hash value of the previous sliding window, i.e. hash(xb) = f(hash(ax), a, b), where f() is fast.

Figure 13: Rabin-Karp sliding window
Rabin-Karp algorithm is simpler to implement, and the probability of false positives can be arbitrarily reduced without effecting the running time of the implementation. It is also possible to reduce the collisions by implementing a Bloom Filter around a rolling hash to reduce the false positives, but at a cost in performance due to multiple hash computations. We have used the Buzhash instead of the Rabin-Karp hash in our rolling hash bloom filter implementation.
Note that even when using the deterministic substring matching algorithm in the previous section, we needed to consult to the corresponding rules before giving the final decision. This suits well with Rabin-Karp algorithm and its probabilistic nature. Furthermore, when the rules are stored in a HashMap with the substrings as the key, we can use the hash() values that we computed using the rolling hash function for finding the appropriate hash bucket in the HashMap, thus saving from an extra hash computation.
Benchmarks
We used Java Micro-benchmarking Harness (JMH) to evaluate the performance of our implementations. JMHallowed us to easily run the benchmarks with different parameters. We were also able to set memory limits for the benchmark JVMs, and JMH made sure that there were sufficient warm-up iterations for the JVM to optimize the code in runtime. Since we are running the measured code in pipelines, the JVM will have ample time to optimize the Java code in runtime, and measuring the performance of the unoptimized code will severely reduce the reliability of the benchmarks for comparing implementations used in this fashion.
Domain Matching
We used pyFST to build OpenFST automata in our batch pipeline, and our Java-based real-time and batch pipelines then load this automaton for labeling the input. We used dk.brics.automaton based Lucene implementation for our automata implementation.
Our benchmarks show that the automaton based solution achieves a 6x speedup over the HashSet based implementation. The benchmarks are computed after 5 warm-up iterations followed by 5 measurement iterations of 1M URL queries for membership in a blacklist of size ~1M domains.
In addition to performace gains, there is another advantage of the automaton based solution: the HashSet based solution only queries the top-level private domain name as opposed to the automaton based solution, which queries all the domain hierarchy including the subdomains. The HashSet implementation misses some of the blacklist entries that the automaton implementation correctly catches. Fixing this behavior would make the HashSet implementation even slower as all the subdomains need to be parsed and queried.
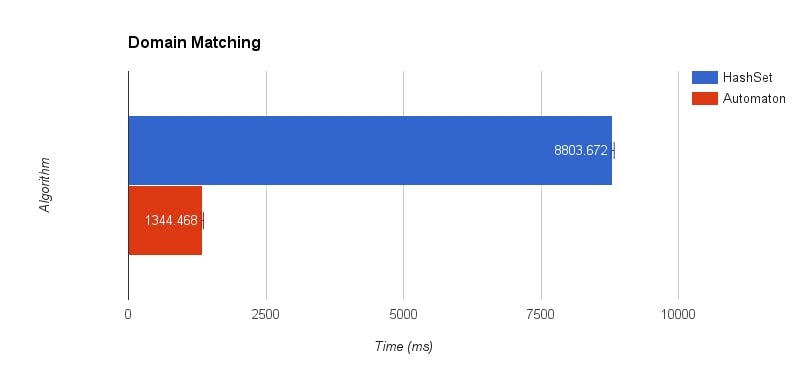
Figure 14: Performance of domain-based NSFW URL matching implementations (shorter is faster)
Benchmark
numURLs
Cnt
Score
Error
Units
domainHashSet
1000000
5
8803.672
± 27.607
ms/iteration
domainAutomaton
1000000
5
1344.468
± 19.025
ms/iteration
Ad URL Matching
In the implementation of automaton based ad classification, we re-used the infrastructure for domain matching, utilizing pyFST, OpenFST, and Lucene. Even when we did not implement the perfect hash optimization or the removal of the transitions to the start state, our benchmarks show that the automaton based solution described here achieves a 2x speedup over a HashMap based implementation.
The Rolling Hash Bloom Filter based solution improves the ad labeling performance further: the automaton based solution is 50% slower than rolling hash solution, which achieves a 3x speedup over the HashMap based solution.
The following benchmarks are computed after 5 warm-up iterations followed by 5 measurement iterations of 1M URL queries for membership in Easylist.
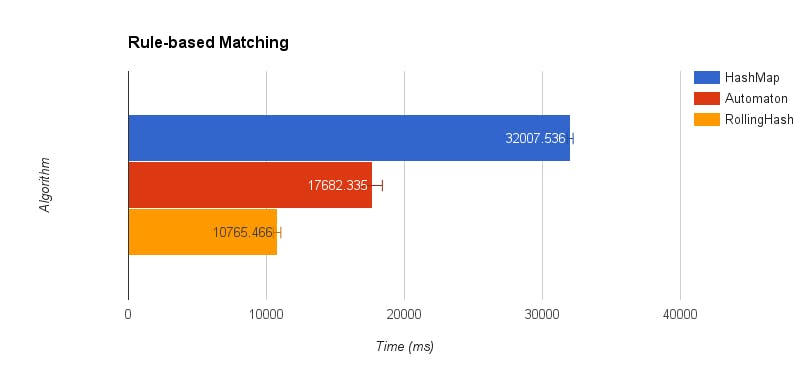
Figure 15: Performance of rule-based ad URL matching implementations (shorter is faster)
Benchmark
numURLs
Cnt
Score
Error
Units
unfilteredAdMatch
1000000
5
32007.536
± 212.058
ms/iteration
automataAdMatch
1000000
5
17682.335
± 712.413
ms/iteration
rabinkarpAdMatch
1000000
5
10765.466
± 276.139
ms/iteration
Conclusion
We have started out with the need to move our classification labeling to the early stages of our analytics pipeline, which required us to investigate ways to measure and compare the performance of implementations and algorithms we use for this task. We found out that JMH not only makes it easy to run benchmarks for different variables and inputs, but also avoids pitfalls in benchmarking of JVM, which uses runtime optimization. In our experiments we found that the finite state machines provide a powerful abstraction and an effective computational tool which we were able to use in both domain-based matching and rule-based matching. OpenFST, pyFST, and Lucene have made it possible for us to easily deploy this tool into use in our analytics pipelines. In order to meet the demands of our pipeline, we pushed performance of rule based matching further by using rolling hash bloom filters. Overall we achieved 6x speedup in domain matching and 3x speedup in rule based matching, along with real-time and batch pipelines that effectively integrates the improved implementations.